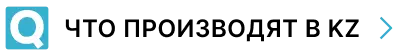+7 (777) 001 44 99
Қазақша
Русский
English
Қазақша
Русский
English
ПОДЕЛИТЬСЯ
Головоломка известного блогера Тима Урбана поставила в тупик многих пользователей Интернета. Задачу из области теории вероятностей блогер опубликовал на своем сайте Waitbutwhy, пишет Lenta.ru.
Головоломка известного блогера Тима Урбана поставила в тупик многих пользователей Интернета. Задачу из области теории вероятностей блогер опубликовал на своем сайте Waitbutwhy, пишет Lenta.ru.
Далее ее условия: Вы идете по дороге, видите сливовое дерево, срываете плод и собираетесь его съесть, но тут приходит хозяин сада, уличает вас в краже и заявляет, что нарушителя ждет смерть.
Однако наказания можно избежать, съев одно из трех предложенных хозяином драже. Леденцы красного, зеленого и синего цвета он выложил на пне. Загвоздка в том, что два из них отравлены. Если вы съедите ядовитый леденец, то умрете, если безвредный - получите прощение и сможете продолжить свой путь.
Предположим, вы выбрали зеленый леденец, но перед тем, как положить его в рот, владелец сливового дерева вдруг объявляет, что решил вам немного помочь и убрать одно из ядовитых драже. После этого он кладет в карман синюю конфету и предлагает вам, если захотите, изменить свой изначальный выбор.
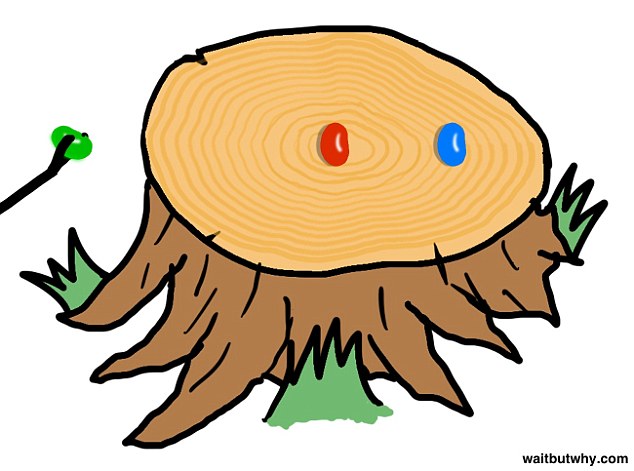
Вопрос заключается в следующем: какова вероятность того, что уже выбранный пленником зеленый леденец ядовит, и, соответственно, оставшийся на пне красный безвреден?
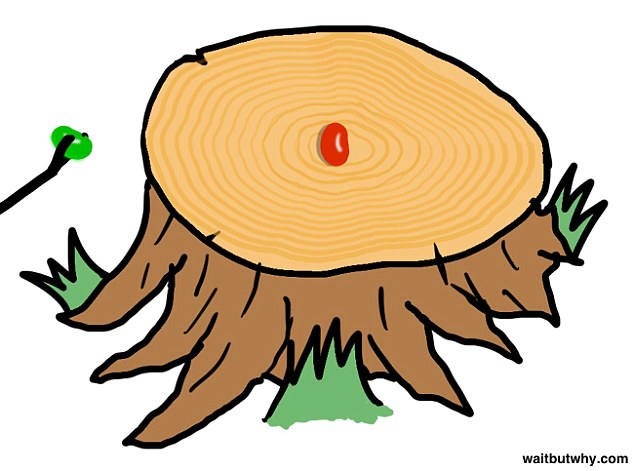
На первый взгляд, соотношение шансов составляет "50 на 50". Именно так решили многие пользователи. Однако на самом деле вероятность того, что первоначально выбранный зеленый леденец ядовит, составляет не 50 процентов, а две трети. Здесь имеет значение тот факт, что хозяин исключил из выбора синий леденец, заявив при этом, что он достоверно отравленный.
Согласно предложенному автором объяснению, изначально выбранное вами драже обладает вероятностью быть безвредным в 1/3, так как на месте остаются еще два. После удаления синей конфеты новой информации о зеленой вы не получаете, а вероятность безопасности красной значительно повышается. Ведь именно она осталась лежать и, возможно, не случайно.
Блогер отметил, что его задача является вариацией парадокса Монти Холла - одной из известных задач теории вероятностей, решение которой, на первый взгляд, противоречит здравому смыслу.
Наиболее распространенная формулировка задачи звучит следующим образом: "Представьте, что вы стали участником игры, в которой нужно выбрать одну из трех дверей. За одной из дверей - автомобиль, за двумя другими дверями - козы. Вы выбираете одну из дверей, например первую, после этого ведущий, который знает, где находится автомобиль, а где - козы, открывает одну из оставшихся дверей, например третью, за которой находится коза. После этого он спрашивает вас - не желаете ли вы изменить свой выбор и выбрать вторую дверь? Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?"
Если игрок меняет дверь после действий ведущего, то имеет наибольшие шансы, то есть с вероятностью 2/3, выиграть при условии изначального выбора проигрышной двери. Дело в том, что изначально выбрать проигрышную дверь можно двумя способами из трех.
